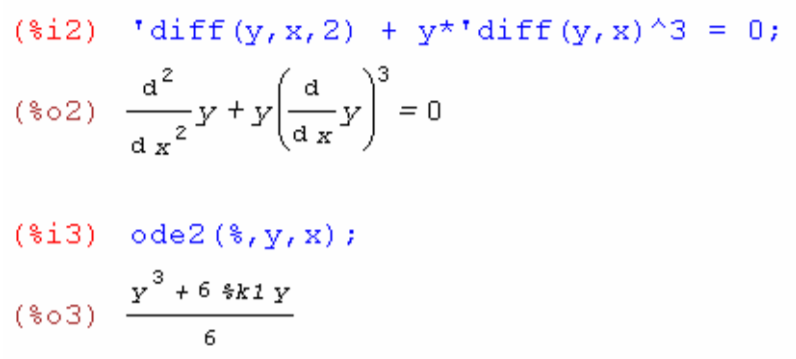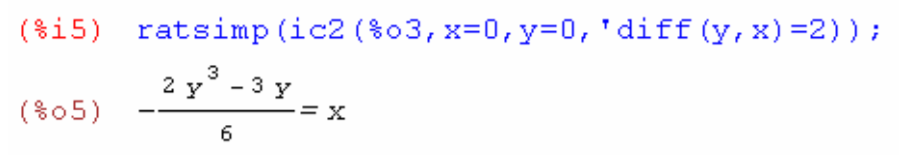Maxima
О программе
Maxima является свободной полнофункциональной системой компьютерной алгебры, она имеет и другие преимущества, основным из которых является сравнительно небольшой объем. Maxima состоит из интерпретатора макроязыка и нескольких поколений пакетов расширений.
Maxima – система для работы с символьными и численными выражениями, включающая дифференцирование, интегрирование, разложение в ряд, преобразование Лапласа, обыкновенные дифференциальные уравнения, системы линейных уравнений, многочлены, множества, списки, векторы, матрицы и тензоры. Maxima производит численные расчеты высокой точности, используя точные дроби, целые числа и числа с плавающей точкой произвольной точности. Система позволяет строить графики функций и статистических данных в двух и трех измерениях. По набору возможностей Maxima близка к таким коммерческим системам, как Maple и Mathematica.
Основными преимуществами программы Maxima являются:
- возможность свободного использования (Maxima относится к классу свободных программ и распространяется на основе лицензии GNU);
- Maxima успешно работает на всех современных операционных системах: Windows, Linux и Unix, Mac OS;
- размер программы (дистрибутив занимает порядка 23 мегабайт, в установленном виде со всеми расширениями потребуется около 80 мегабайт);
- широкий класс решаемых задач;
- возможность работы как в консольной версии программы, так и с использованием одного из графических интерфейсов (xMaxima, wxMaxima или как плагин (plug-in) к редактору TexMacs);
- расширение wxMaxima (входящее в комплект поставки) предоставляет пользователю удобный и понятный интерфейс, избавляет от необходимости изучать особенности ввода команд для решения типовых задач;
- интерфейс программы на русском языке;
- наличие справки и инструкций по работе с программой (русскоязычной версии справки нет, но в сети Интернет присутствует большое количество статей с примерами использования Maxima);
Решение задач алгебры
1. Найти частное и остаток от деления одного многочлена x^3-2 на другой x-1
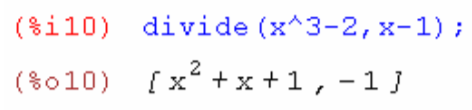
Первый элемент полученного массива – частное, второй – остаток от деления.
2. Разложить на множители выражения ax^2+ax+a и x^2+2x+1
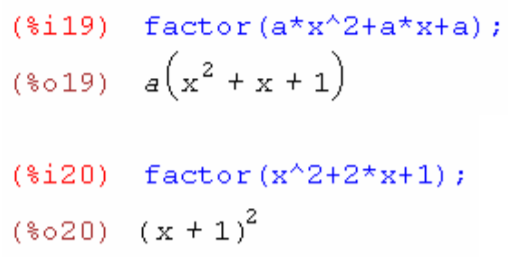
3. Раскрыть скобки (2+3x)(3y+5x)
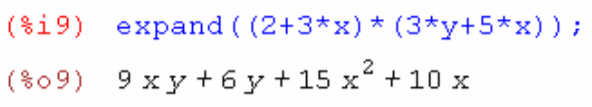
4. Найти наибольший общий делитель многочленов x^3-1,x^2-1 и x-1
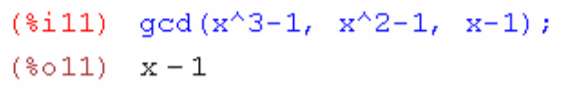
5. Упростить выражение 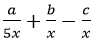
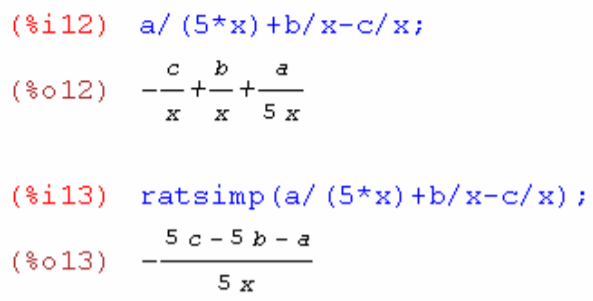
6. Разложить на простые дроби 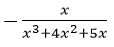
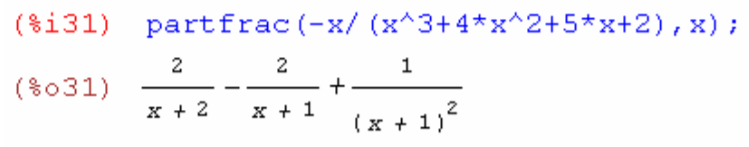
7. Упростить тригонометрическое выражение 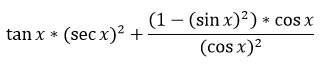
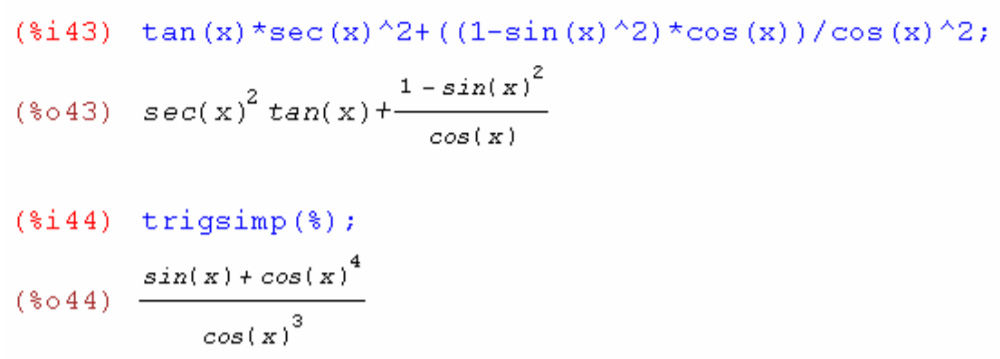
8. Преобразовать тригонометрическое выражение 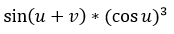

9. Решить систему линейных алгебраический уравнений 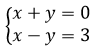
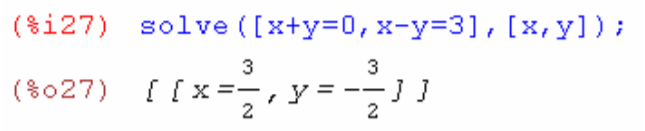
(в качестве параметров в первых квадратных скобках указывается список уравнений через запятую, во-вторых – список переменных, через запятую)
10. Решить систему нелинейных алгебраических уравнений 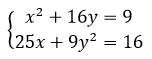

(в качестве параметров в первых квадратных скобках указывается список уравнений через запятую, во-вторых – список переменных, через запятую)
11. Перемножить матрицы 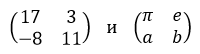


12. Найти определитель матрицы 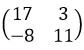

13. Определить ранг матрицы 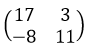

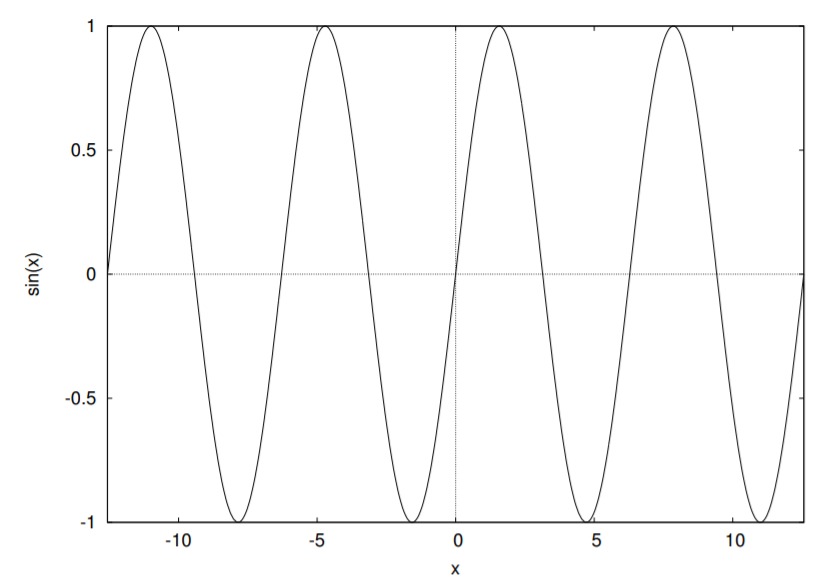
14. Построить график функции y = sin(x) на отрезке [-4π,4π].
Синтаксис:
plot2d(f(x),[x,a,b],опции)или plot2d(f(x),[x,a,b],[y,c,d],опции)
Опции не обязательны, однако, для изменения свойств графика их нужно задавать. Параметр [y,c,d] можно не задавать, тогда высота графика выбирается по умолчанию.
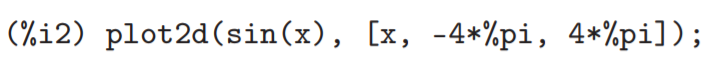
Решение задач математического анализа
1. Найти первую производную функции 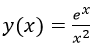
Алгоритм решения:
- Ввести функцию y(x):=exp(x)/x^2; (в отличие от присвоения значения переменной, здесь используется комбинация символов «:=» (двоеточие и равно))
- Найти производную функции, используя команду diff(функция,переменная,порядок производной); В случае первой производной ее порядок можно не указывать.

2. Вычислить неопределенный интеграл ∫(x^2+5x+3)dx
Для нахождения неопределенного интеграла в качестве аргументов указывается функция и переменная интегрирования.
Синтаксис: integrate(функция,переменная);
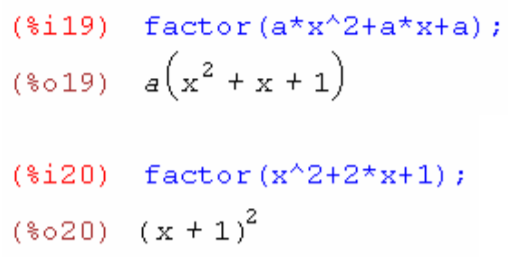
3. Вычислить определенный интеграл 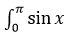
При нахождении значения определенного интеграла помимо рассмотренных параметров указываются пределы интегрирования.
В качестве пределов интегрирования могут фигурировать бесконечность (inf) и минус бесконечность (minf).
Синтаксис: integrate(функция,переменная,левый предел,правый предел);

4. Найти предел 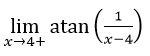
Синтаксис: limit(функция,переменная,значение,слева/справа);
Предел слева обозначается minus, а справа – plus (необязательный параметр)

5. Разложить функцию sin(x)+ax+1 в ряд Тейлора по степеням x+1 до третьей степени.
Синтаксис: taylor(функция,x,a,n)
Параметр n определяет, до какой степени (x-a) находить решение.

6. Решить дифференциальное уравнение первого порядка 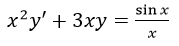 при
при 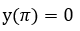
Алгоритм решения:
Ввести ДУ, обращая внимание на одинарную кавычку (она позволяет отображать, но не вычислять некоторое выражение).
Затем применить функцию ode2(уравнение,зависимая переменная,независимая переменная)
Подставить значение начального условия задачи, воспользовавшись функцией ic1
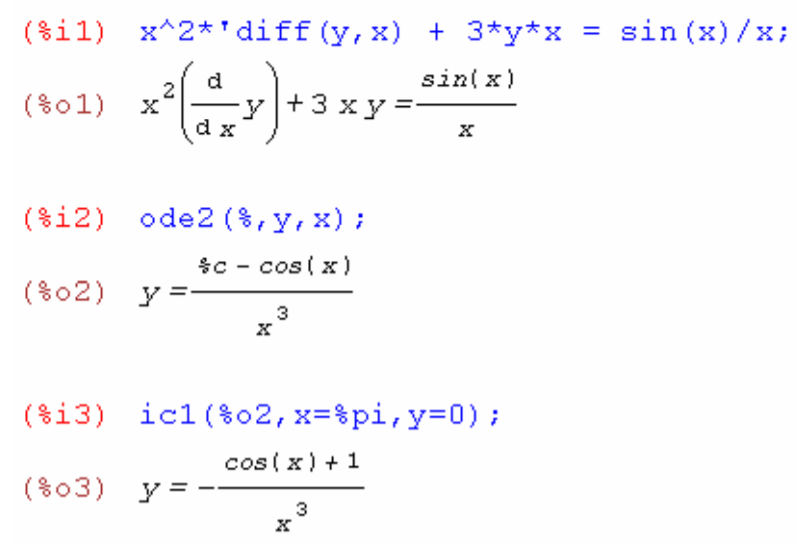
7. Решить дифференциальное уравнение второго порядка 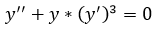 при начальных условиях
при начальных условиях 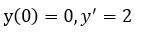
Алгоритм решения:
Ввести ДУ, обращая внимание на одинарную кавычку (она позволяет отображать, но не вычислять некоторое выражение).
Затем применить функцию ode2(уравнение,зависимая переменная,независимая переменная)
Для подстановки начального условия используется функция ic2, сразу же можно упростить полученный ответ при помощи функции ratsimp