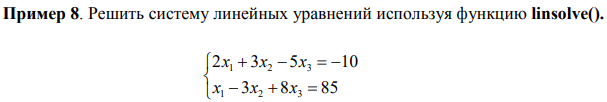Scilab
О программе
Scilab - одна из мощнейших и наиболее функциональных программ. Представляет собой интерпретируемый язык программирования и множество математических пакетов, которые позволяют быстро получить правильное решение непростых уравнений и задач.
Задачи, решаемые в Scilab
- 2D и 3D графики, анимация
- Линейная алгебра, разреженные матрицы (sparse matrices)
- Обработка сигналов
- Параллельная работа
- Статистика
- Интерфейс к Fortran, Tcl/Tk, C, C++, Java, LabVIEW
- Полиномиальные и рациональные функции
- Интерполяция, аппроксимация
- Работа с компьютерной алгеброй
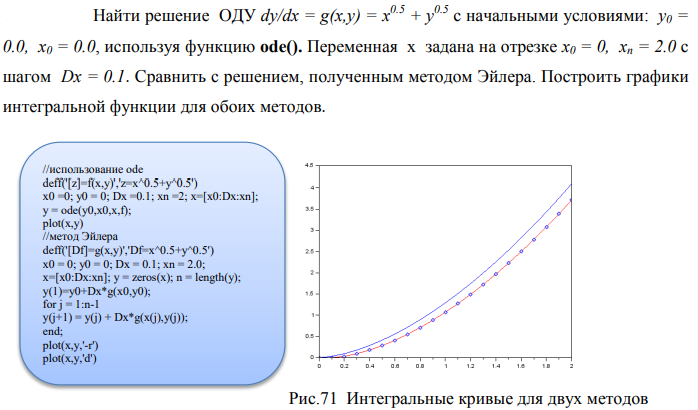
- Симуляция: решение ОДУ и ДУ
- Scicos: гибрид системы моделирования динамических систем и симуляции
- Дифференциальные и не дифференциальные оптимизации
Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.
Особенности СКА
Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.
Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.
Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.
Для численных расчётов используются библиотеки Lapack, LINPACK, ODEPACK, Atlas и другие.
В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.
Алгоритмы решения задач
- Определить область задачи.
- Составить математическую модель.
- Ввести условия.
- Используя СКА, найти решение.
- Проанализировать полученные результаты.
Преимущества
- функциональность;
- работа в режиме интерпретатора;
- Бесплатность;
- Свободность (с версии 5.0);
- большое количество справочной информации;
- программирование алгоритмов через встроенный процедурный язык;
- поддержка языков высокого уровня, т. е. программирование без жёсткой привязки к языку;
- Маленький размер — дистрибутив 4 версии занимал менее 20 МБ.
- Возможность запуска в консоли без использования графического интерфейса, в том числе в версии под Windows. Это позволяет производить автоматизированные вычисления, есть пакетный режим.
Недостатки
- нет такой визуализации программирования как в Mathematic;
- система использует прежде всего численные подходы, для вычисления, что может сказаться на точности.
- достаточно малое количество инструментов в Xcos для построения схем, что усложняет разработку специфических и сложных систем, например систем векторного управления асинхронным двигателем.
Примеры решения задач
Пример 1. Решить тригонометрическое уравнение: sin(x)+cos(x)=1

Пример 2. Вычислить значение сложного математического выражения:
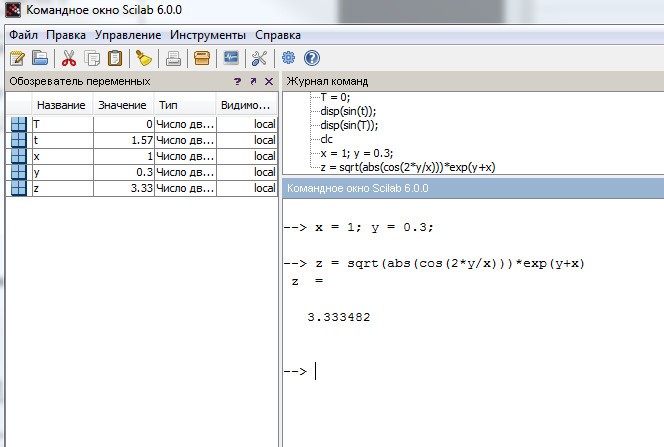
Пример 3. Вычислить значения выражений: с=3+а+2*b, c=2*(a+b)-4 при а=1, b=1.

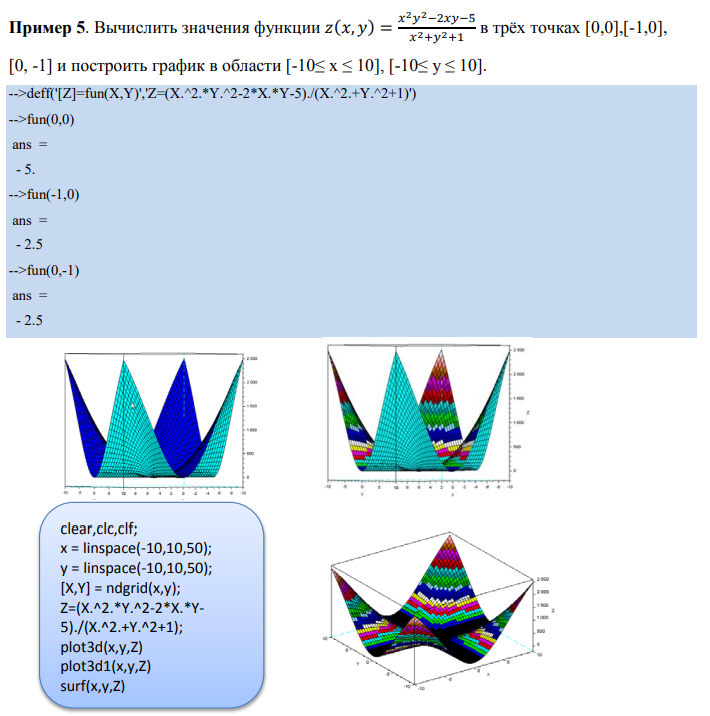
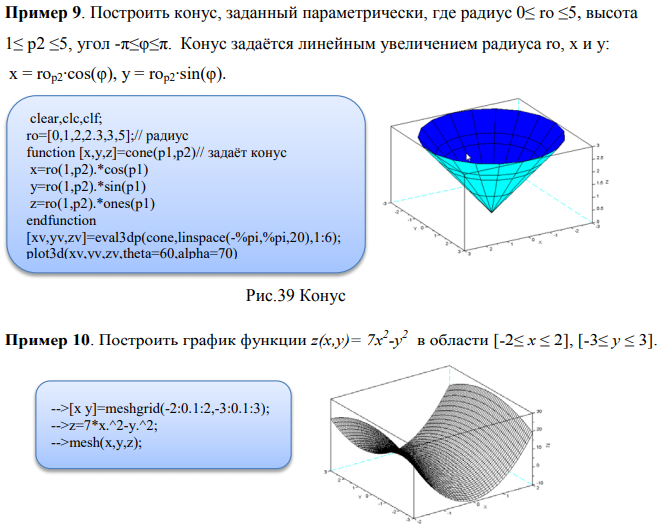
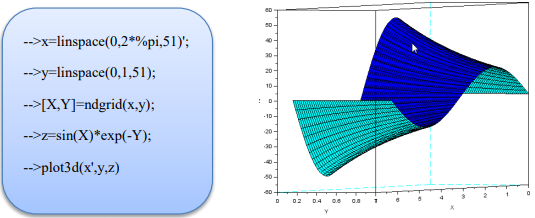
Пример 4. Вычислить значения функции z=x*y в области и построить график этой функции.

6. Работа с полиномами. Создать полином, имеющий корни 3 и 2 с символьной переменной х.